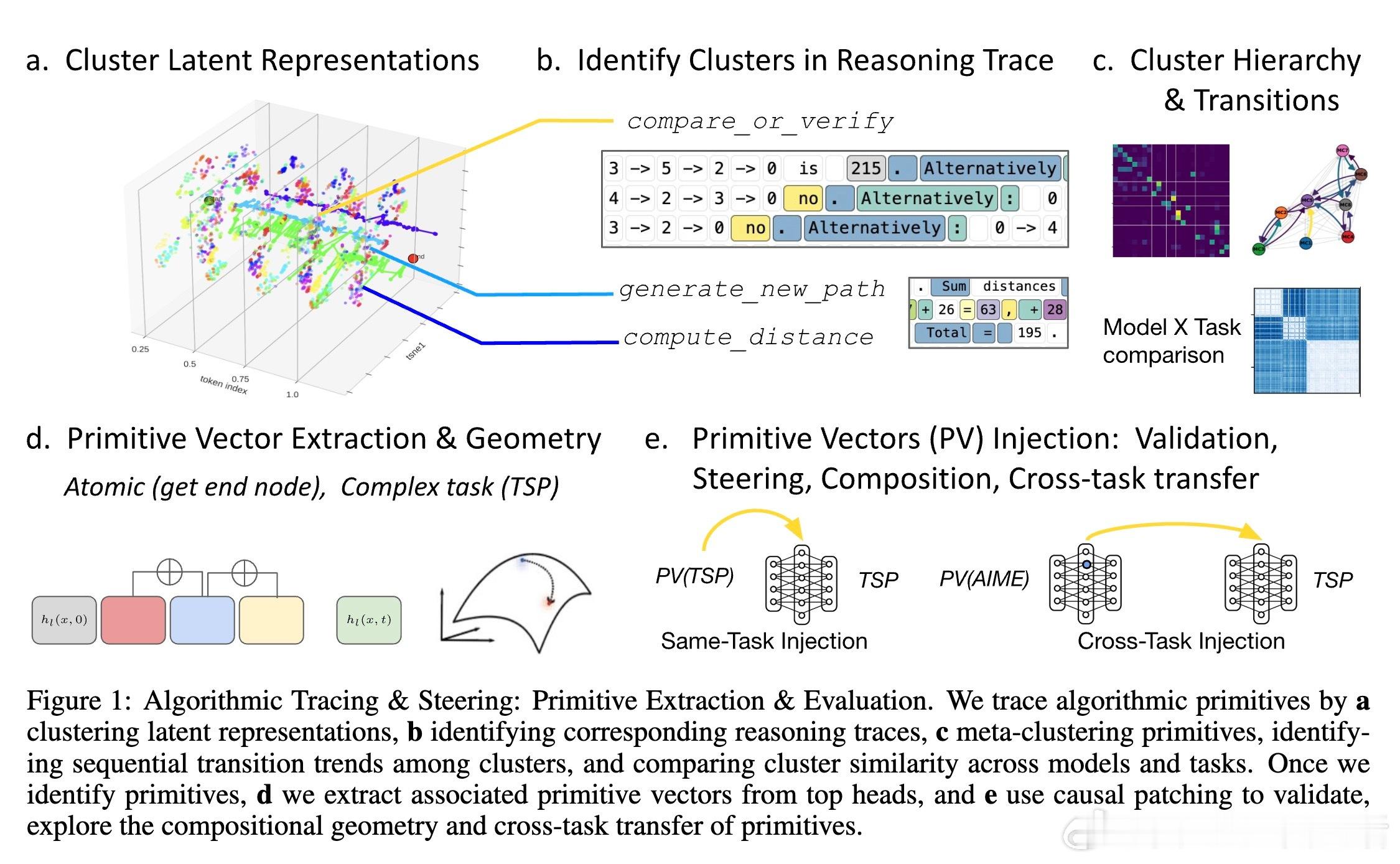
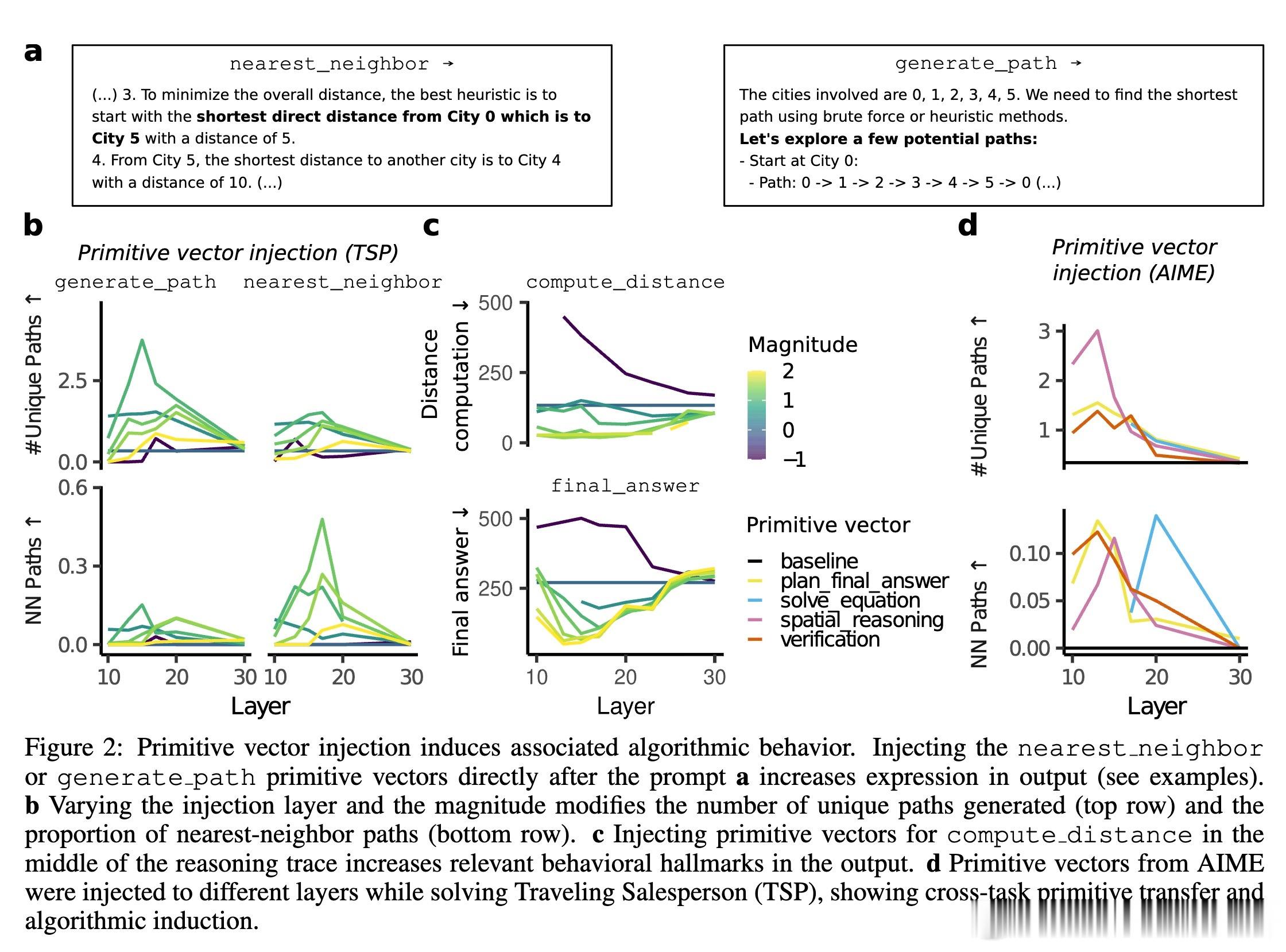
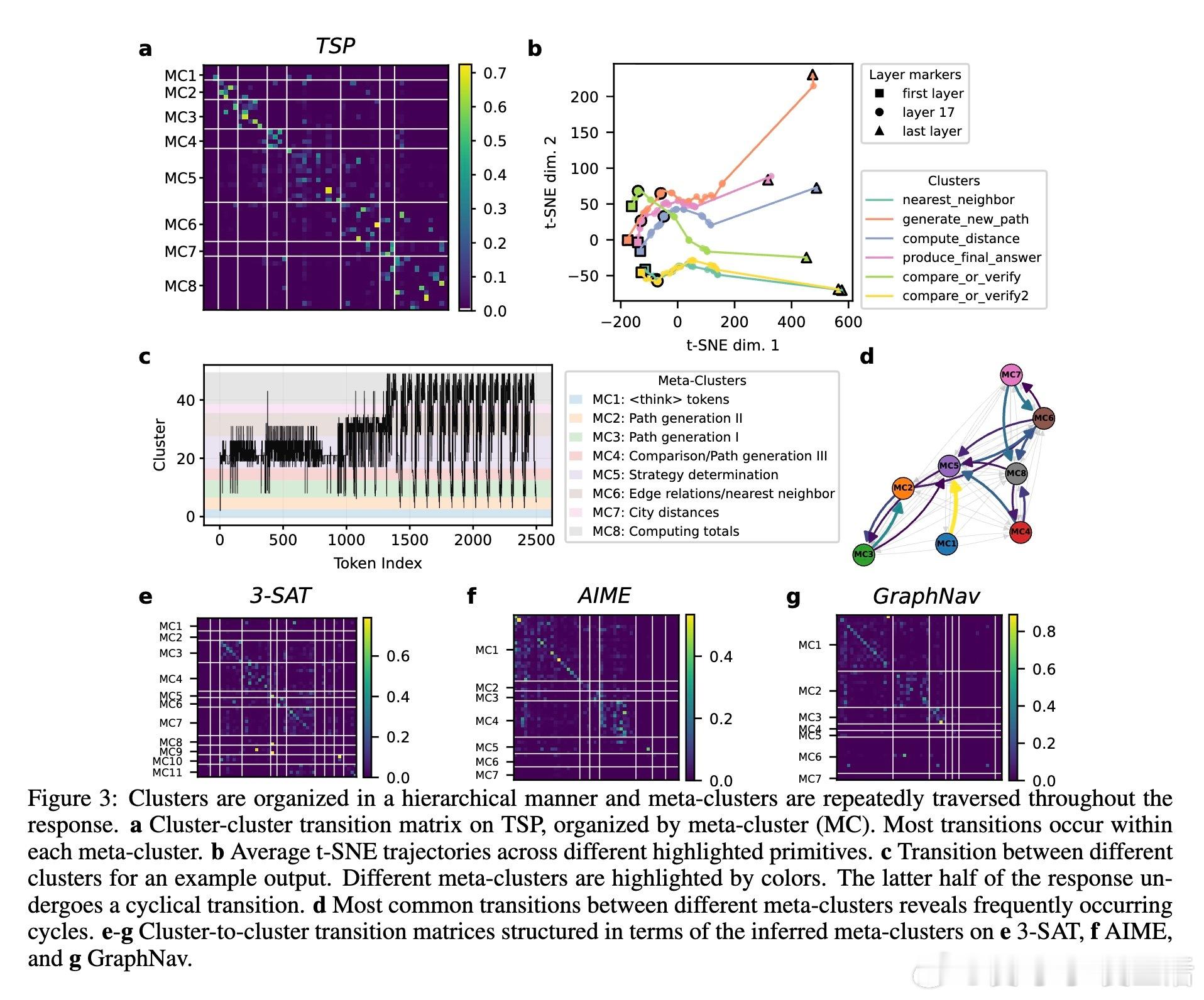
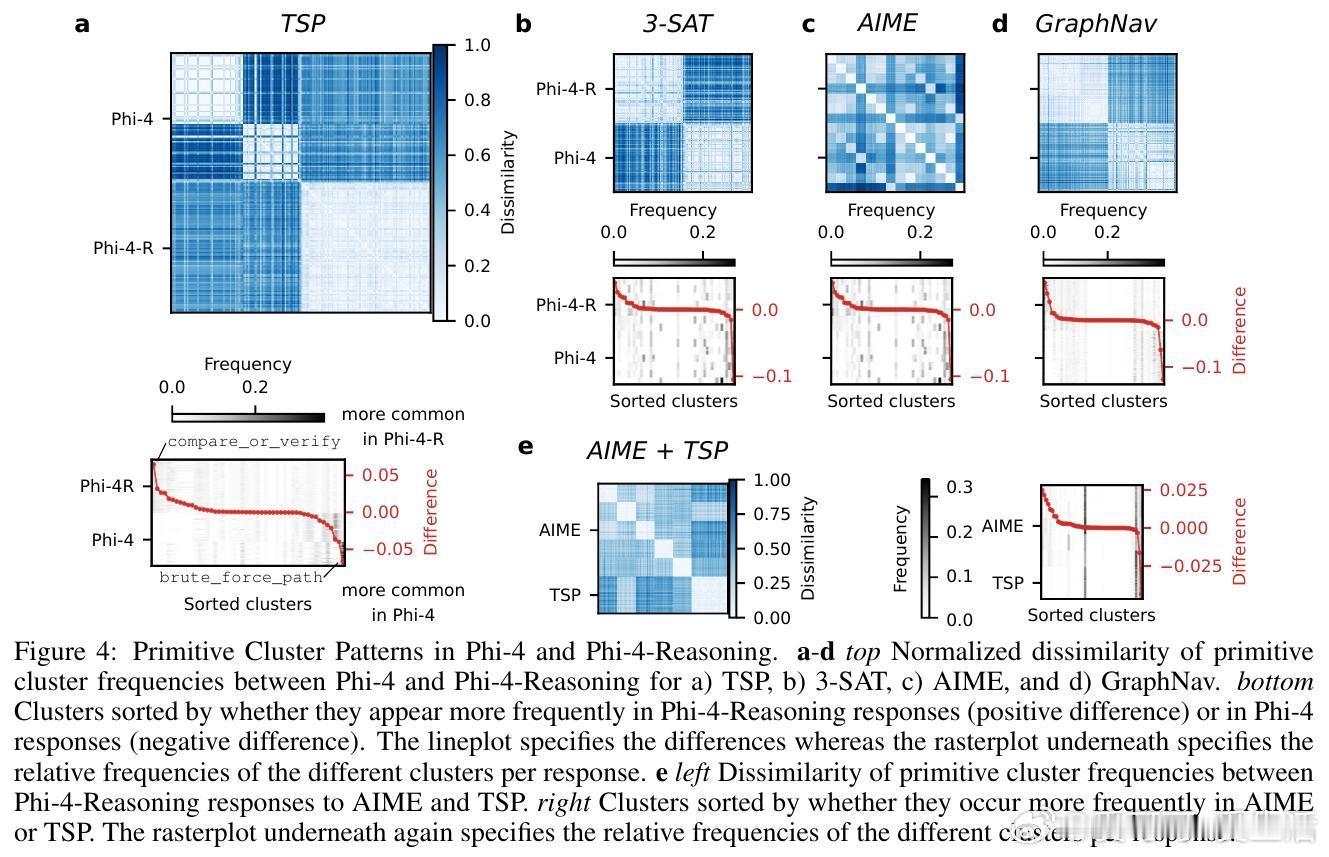
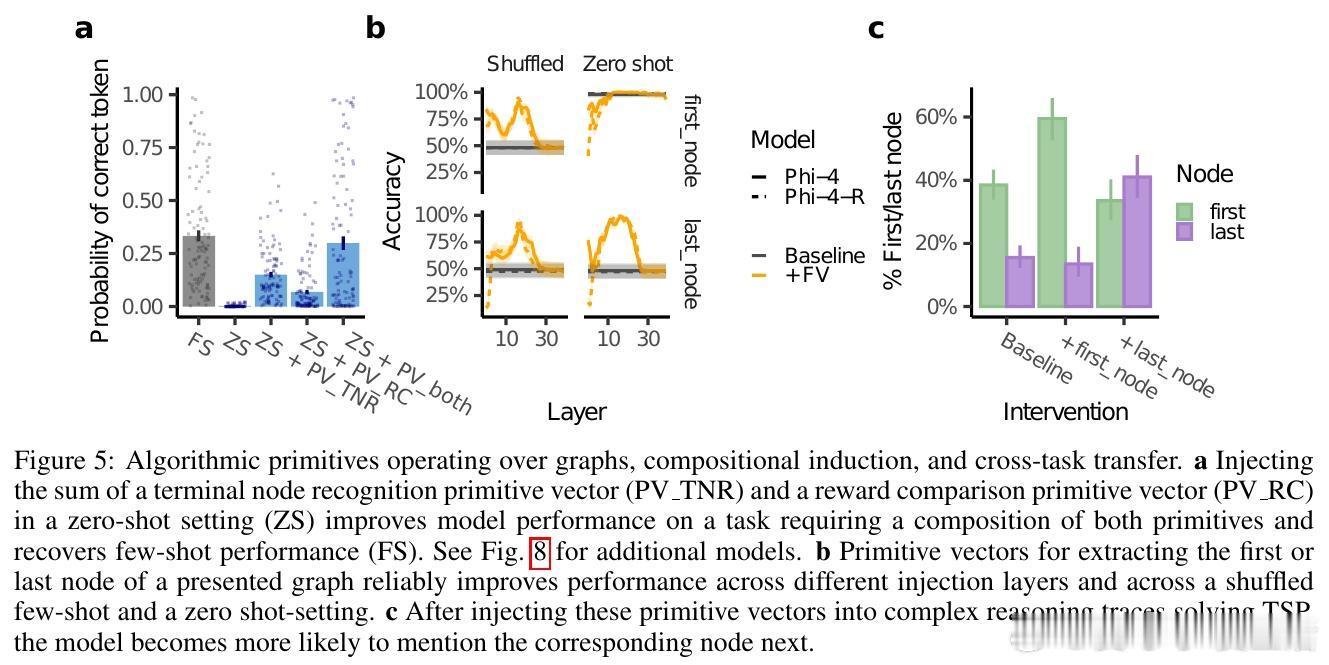
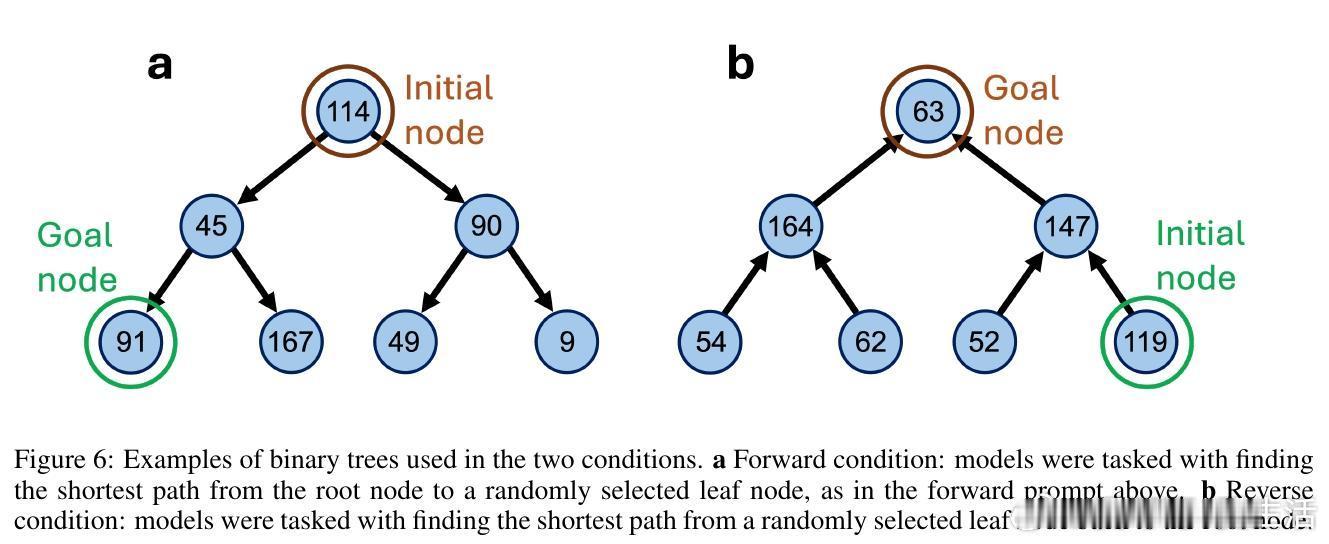
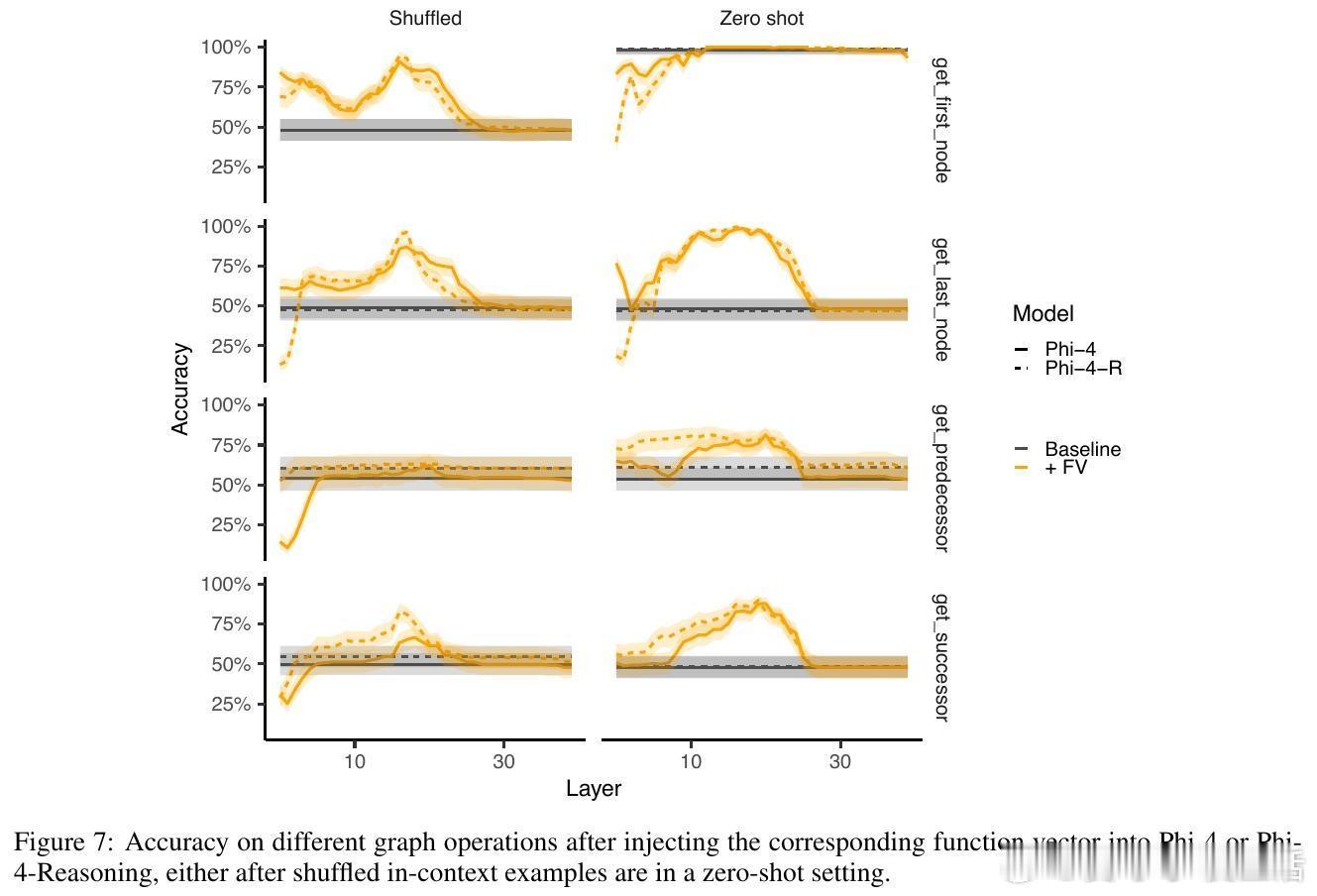
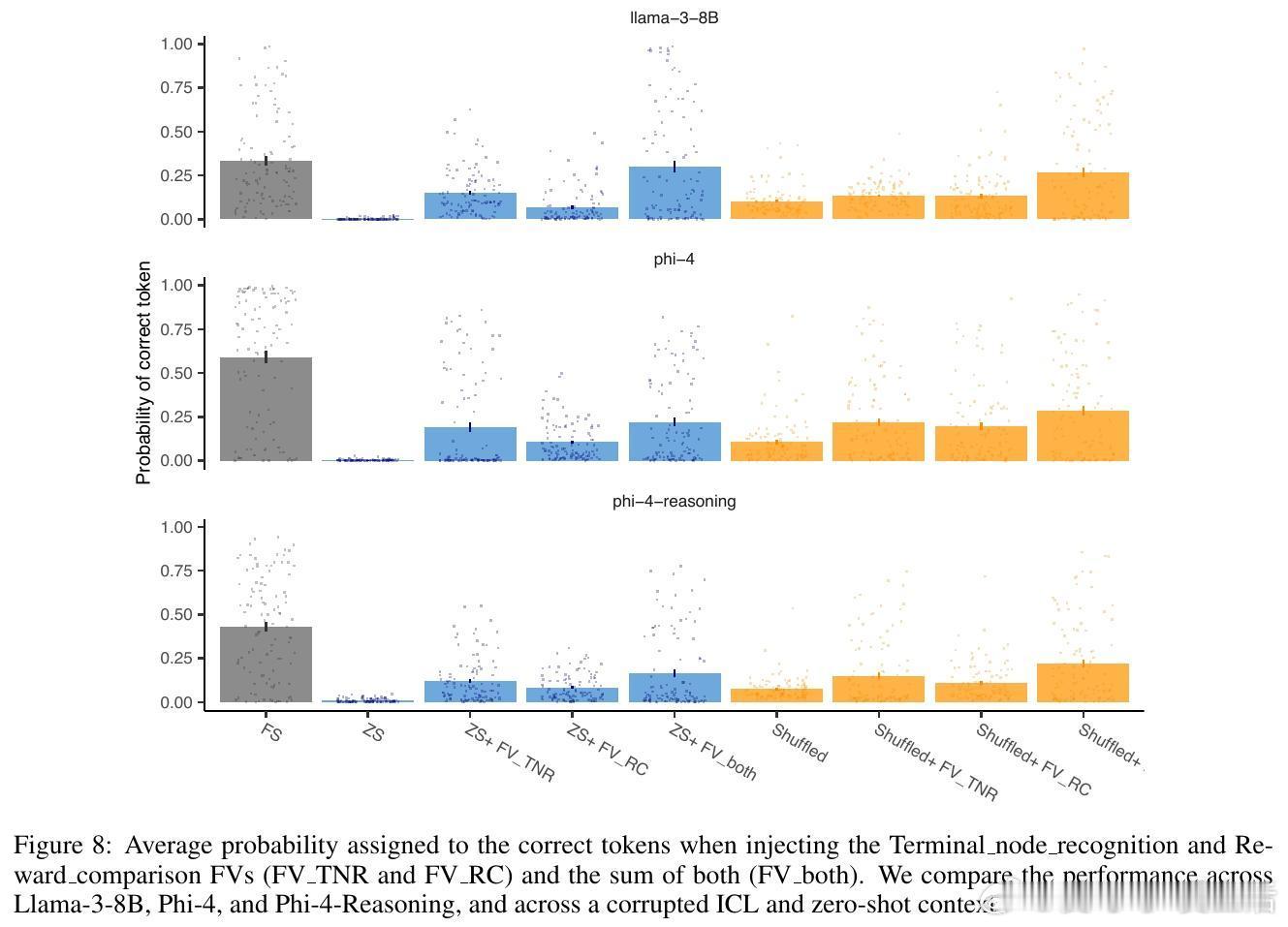
[LG]《Algorithmic Primitives and Compositional Geometry of Reasoning in Language Models》S Lippl, T McGee, K Lopez, Z Pan... [Columbia University & University of California Los Angeles & Harvey Mudd College] (2025)
本文提出了一套全新的框架,揭示大型语言模型(LLM)如何通过“算法原语”(algorithmic primitives)实现复杂多步推理。该工作不仅识别了模型内部激活模式与推理步骤的对应关系,还通过向模型中注入“原语向量”精准操控推理行为,验证了这些原语的因果作用。
主要贡献:
1. 跨任务与跨模型系统性识别了算法原语,如“最近邻搜索”、“路径生成”、“距离计算”、“验证比较”等,覆盖旅行商问题(TSP)、3SAT、美国数学邀请赛(AIME)、图导航等多样推理任务。
2. 提出原语向量的几何组合方法,通过向量加减与标量乘法展示推理步骤在激活空间的线性组合和可控性,体现了推理的“几何逻辑”。
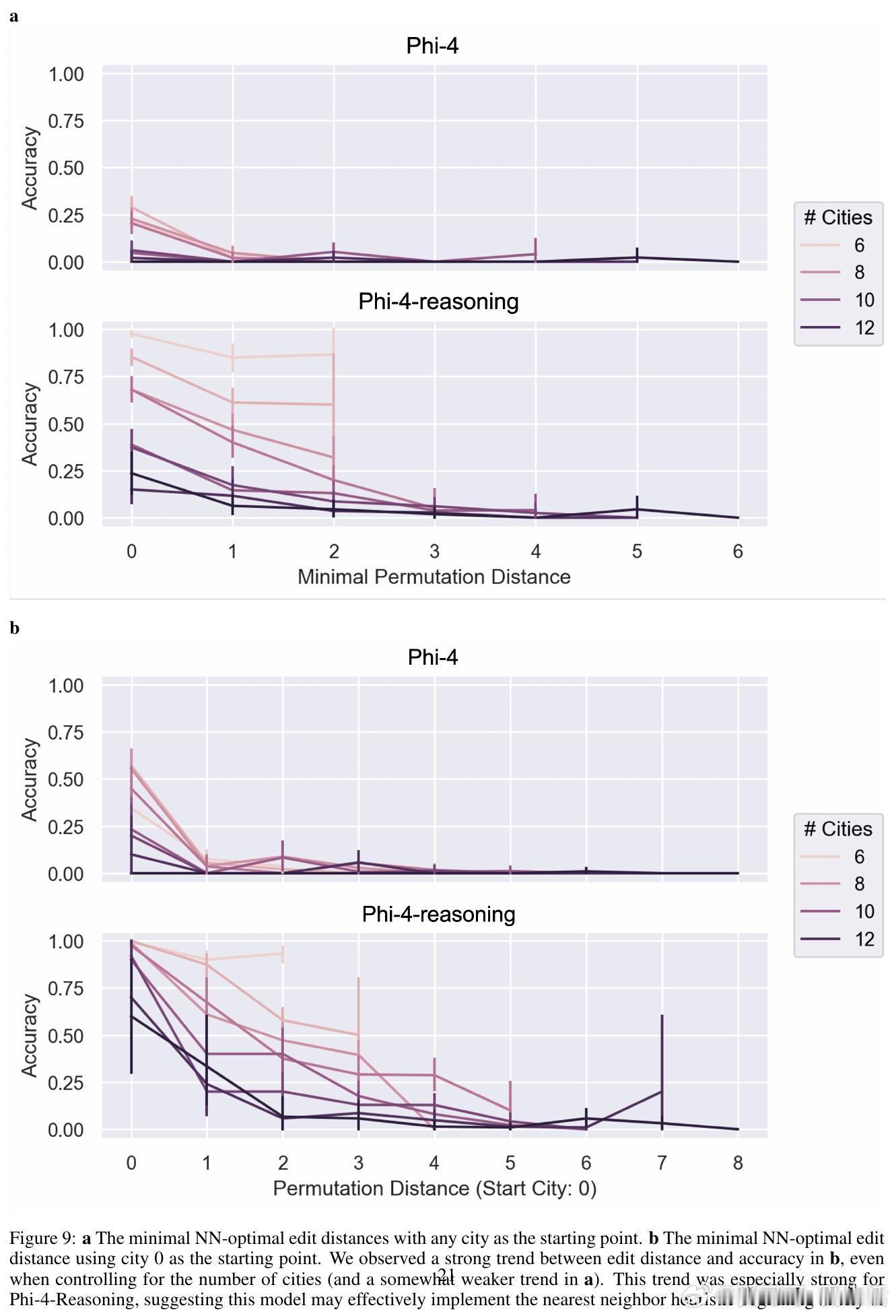
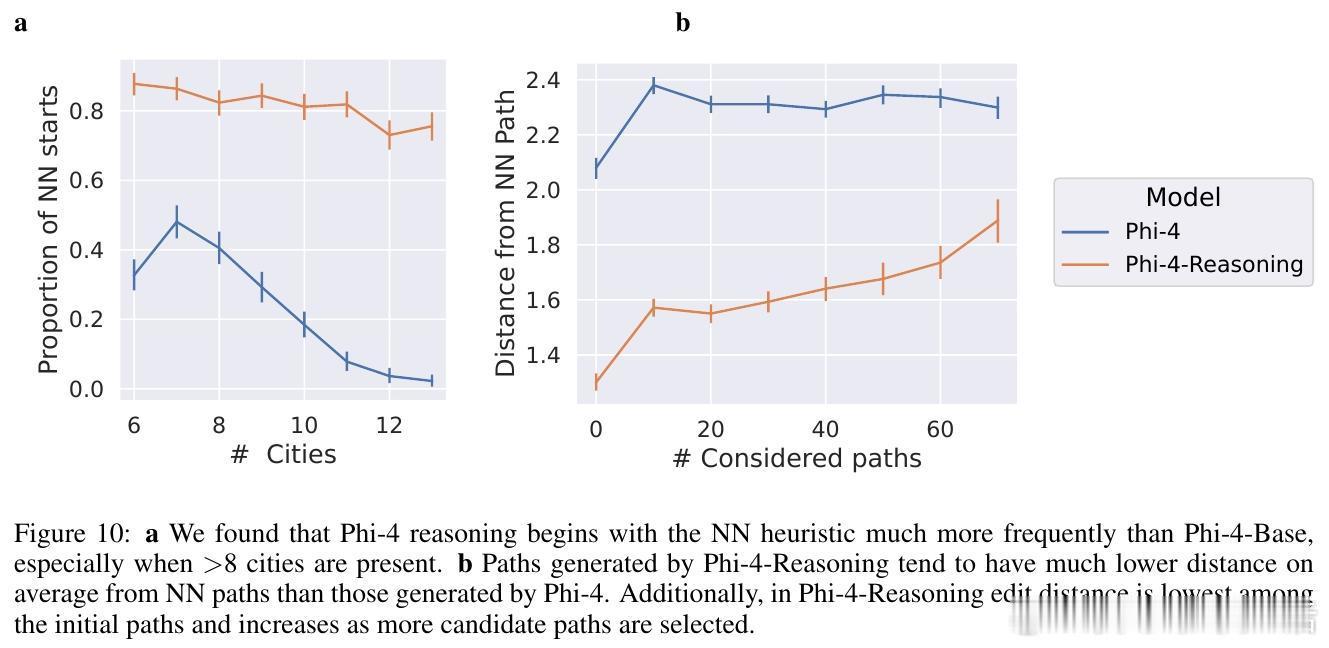
3. 通过对比基础模型Phi-4与推理微调模型Phi-4-Reasoning,发现后者展现出更系统的验证与路径生成原语使用,体现了微调带来的算法泛化能力提升。
4. 实验表明,从一个任务中提取的原语向量能够迁移至另一个任务,促进跨域推理能力,揭示了潜在的通用算法构建块。
5. 通过“算法追踪与引导”框架,结合聚类分析与注意力头激活,建立了从内部表征到行为输出的因果链路,开辟了模型机制解释的新路径。
研究启示:
- LLM的多步推理并非简单记忆,而是通过可组合的最小计算单元实现,具备一定的抽象与泛化能力。
- 推理微调优化了模型对这些原语的系统调用,提升了模型在未见任务上的表现稳定性和合理性。
- 激活空间的几何结构为未来设计更高效、更可解释的推理模型提供了理论基础和实践工具。
未来展望:
- 拓展原语库,深化非线性组合及多模态推理的几何分析。
- 利用算法原语实现针对性的训练和微调,推动模型自我改进和算法自玩。
- 构建人机推理对齐机制,促进模型推理与人类认知的协同发展。
全文地址:arxiv.org/abs/2510.15987
此研究为理解和提升大型语言模型推理能力提供了结构化、可解释的算法视角,推动了AI可解释性与推理性能的双重进步。值得AI研究者和工程实践者深入关注。