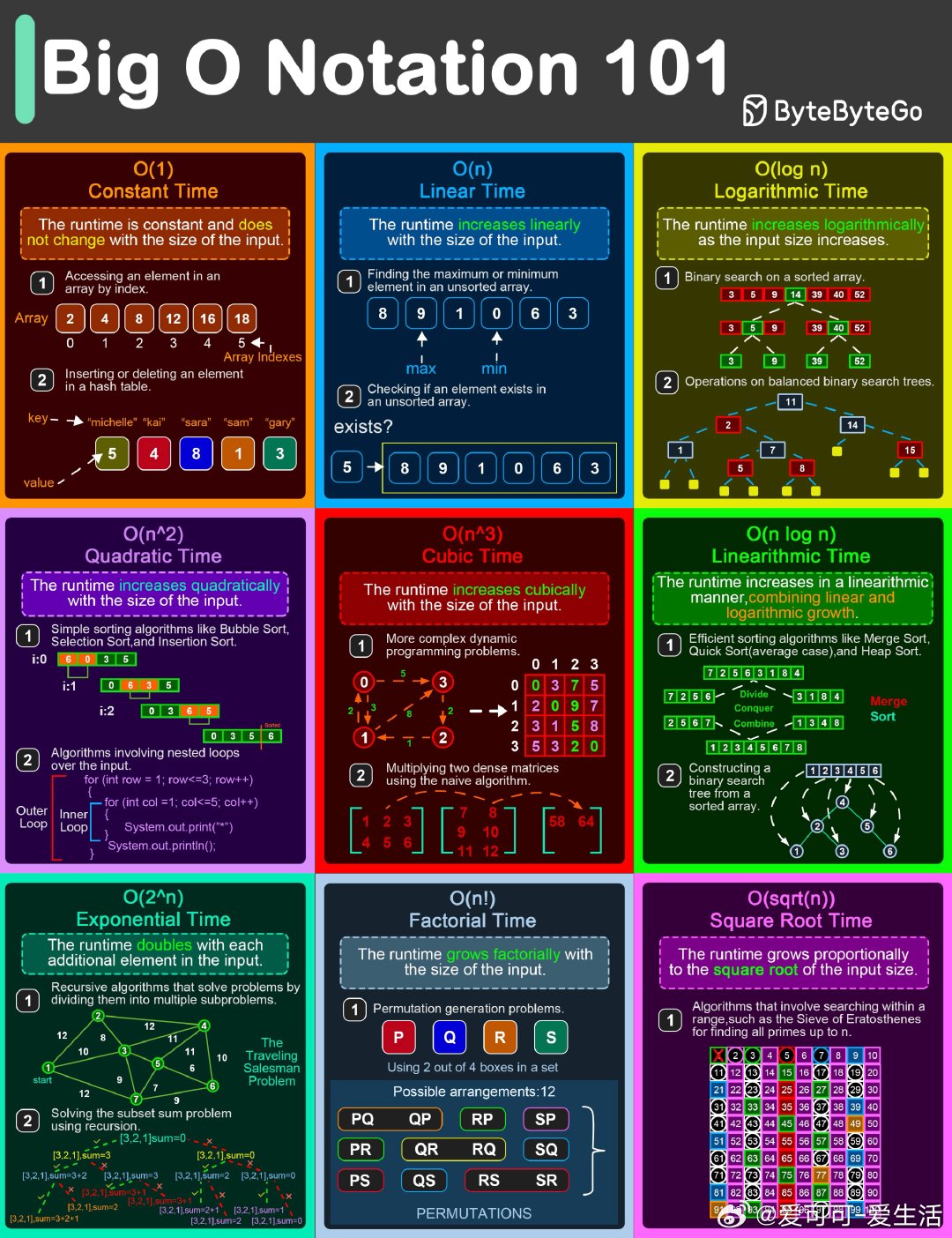
大多数人很难直观理解算法复杂度,这张图用简明示例详细阐释了不同Big O符号的含义和对应的算法行为。
• O(1) 常数时间:无论输入多大,运行时间保持不变。典型例子是通过索引访问数组元素或哈希表插入删除。
• O(n) 线性时间:运行时间与输入规模成正比增加,比如遍历数组寻找最大/最小值,或者判断元素是否存在。
• O(log n) 对数时间:输入规模每增加一倍,运行时间增加一个常量单位。示例包括有序数组的二分查找和平衡二叉搜索树操作。
• O(n²) 平方时间:运行时间随着输入规模的平方增长,常见于嵌套循环排序算法,如冒泡排序、选择排序。
• O(n³) 立方时间:运行时间增长更快,适用于复杂动态规划问题和矩阵乘法的朴素算法。
• O(n log n) 线对数时间:结合线性与对数增长,效率较高的排序算法如归并排序、快速排序、堆排序都属于此类。
• O(2^n) 指数时间:运行时间随着每增加一个输入元素翻倍,典型递归分治算法,如旅行商问题和子集和问题。
• O(n!) 阶乘时间:运行时间以输入规模的阶乘速度增长,排列组合问题的典型代表。
• O(√n) 平方根时间:运行时间按输入规模平方根比例增长,用于范围内搜索,代表算法如埃拉托斯特尼筛法。
心得:
1. 规模增长带来的时间成本差异远超直觉,尤其从线性到指数、阶乘增长,算法性能天壤之别。
2. 选择合适的算法结构和数据结构(如哈希表、平衡树)能大幅降低复杂度,提升效率。
3. 复杂度分类帮助评估算法在实际应用中的可行性,避免盲目使用高复杂度算法。
算法 计算复杂度 大O符号 编程基础 数据结构