详解微积分物理意义一图讲透微积分
很多人觉得微积分抽象、难懂,其实每个符号背后都有物理意义。
而这张图,把微积分两大核心公式:微分和定积分详细拆解了。如果你以前学数学一脸懵,看完这张图会有种“原来如此”的感觉。
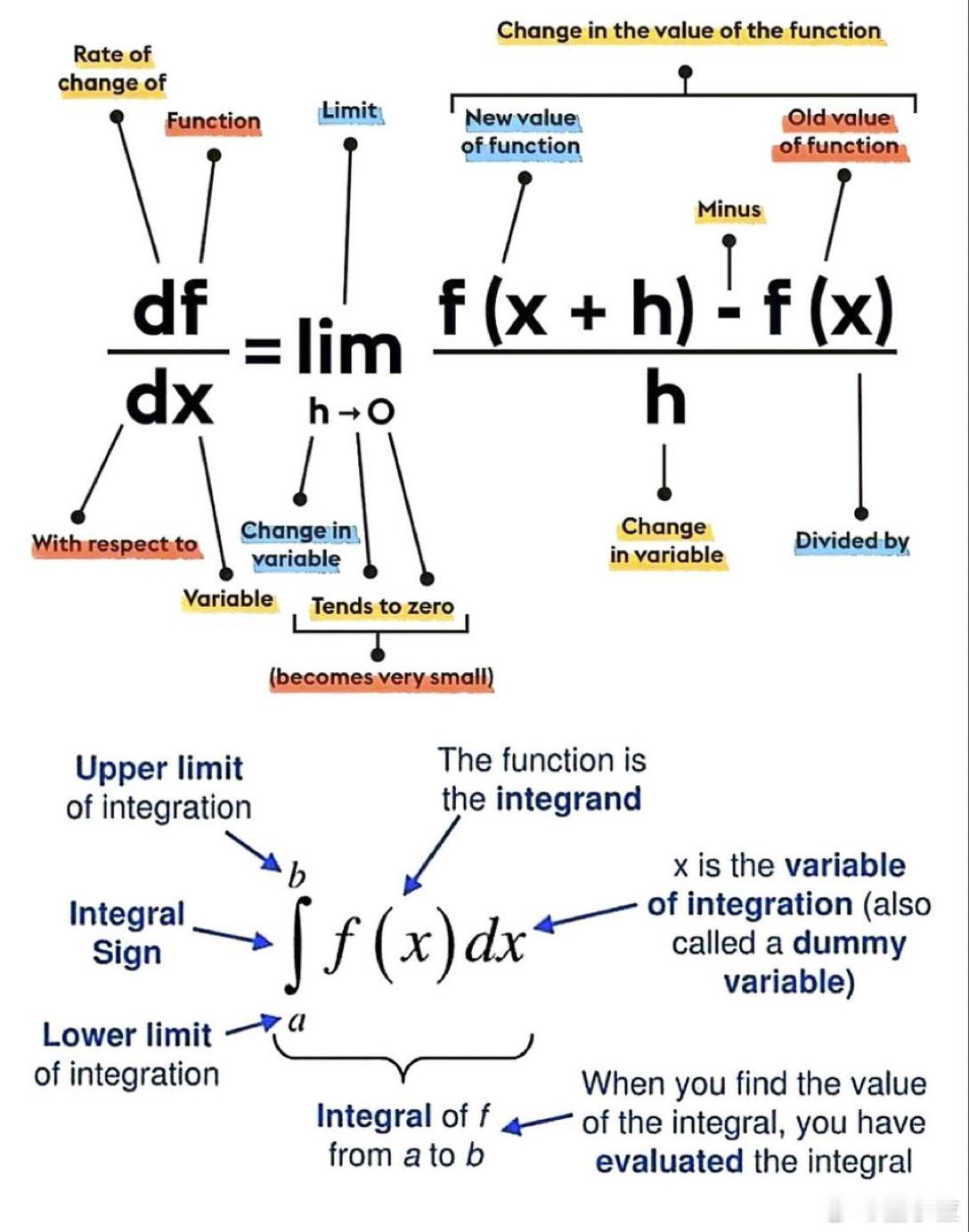
1)先来看上半部分:微分(导数)公式
这是描述“变化率”的公式,写作:
df/dx = lim (h→0) [f(x+h) - f(x)] / h
意思是:x变化非常非常小的时候,f的变化率是多少?
逐一解释下图中各部分含义:
- `df/dx`:表示函数f对x的导数,也就是x变化时,f是怎么跟着变的
- `df`:f这个函数的变化量
- `dx`:x的变化量
- 合起来就是“f相对于x的变化率”
- `lim`:极限的意思
- 它的作用是让`h`变得无限小,趋近于0,但不是等于0
- `h → 0`:表示h趋近于0,也就是“变化非常非常小”
- `f(x + h)`:x增加一点点h之后,函数的新值
- `f(x)`:原来的函数值
- `f(x + h) - f(x)`:表示函数值的变化量
- `/ h`:再除以h(x的变化量),就得到了平均变化率
- 当h趋近于0时,这个“平均”就变成了“瞬时”,这就得到了导数。
总的来说,导数是用来回答这个问题的:“当x轻轻变一下,f会怎么变?”
比如:
- 汽车的位移函数f(x)的导数是速度(每单位时间位移变化);
- 速度的导数是加速度(速度怎么变)。
2)再看下半部分:定积分公式
这是另一个微积分的核心,写作:
∫[a到b] f(x) dx
意思是:从a到b,把f(x)这个函数的所有“小片段”加起来
图中每部分解释如下:
- `∫`:这个符号就是积分符号,长得像个拉长的S,表示“求和”(sum)
- `f(x)`:被积函数,积分时要“加起来”的部分,通常代表“每单位的量”
- `dx`:x的变化单位,表示我们是“沿着x轴”在加每一小段值
- 也叫积分变量,或“哑变量”(dummy variable)
- `a`、`b`:积分的起点和终点,表示我们只在这个区间里计算总量
- 整个表达式:从x=a加到x=b,把f(x)在每一小段x上的“值”都加起来
- 积分的结果是一个数,表示“总变化量”,这就叫“积分值”
比如:
- 已知速度是时间的函数v(t),那么∫v(t)dt就表示总位移;
- 已知功率是时间的函数,积分一下就得出总能量消耗;
- 已知某物体密度函数,积分就能求出总质量。
总结一下:
- 上面的导数公式告诉你“某个瞬间变化多快”
- 下面的积分公式告诉你“整体上变化了多少”
一个是瞬时变化,一个是累计总量,像是微积分这门语言的两面。物理、经济、工程、机器学习、动画模拟……到处都是它的影子。
这也是数学的魅力:每个符号都不是随便写的,它们都能讲出一个完整的故事。