[LG]《Global Dynamics of Heavy-Tailed SGDs in Nonconvex Loss Landscape: Characterization and Control》X Wang, C Rhee [University of Amsterdam & Northwestern University] (2025)
深度学习中,随机梯度下降(SGD)因其能避免“尖锐”局部极小点而广泛受到关注,这与模型的泛化能力密切相关。本文深入探索了带截断重尾噪声的SGD在多极小点非凸损失景观中的全球动态,并提出基于此的优化策略,有效提升模型泛化性能。
核心贡献包括:
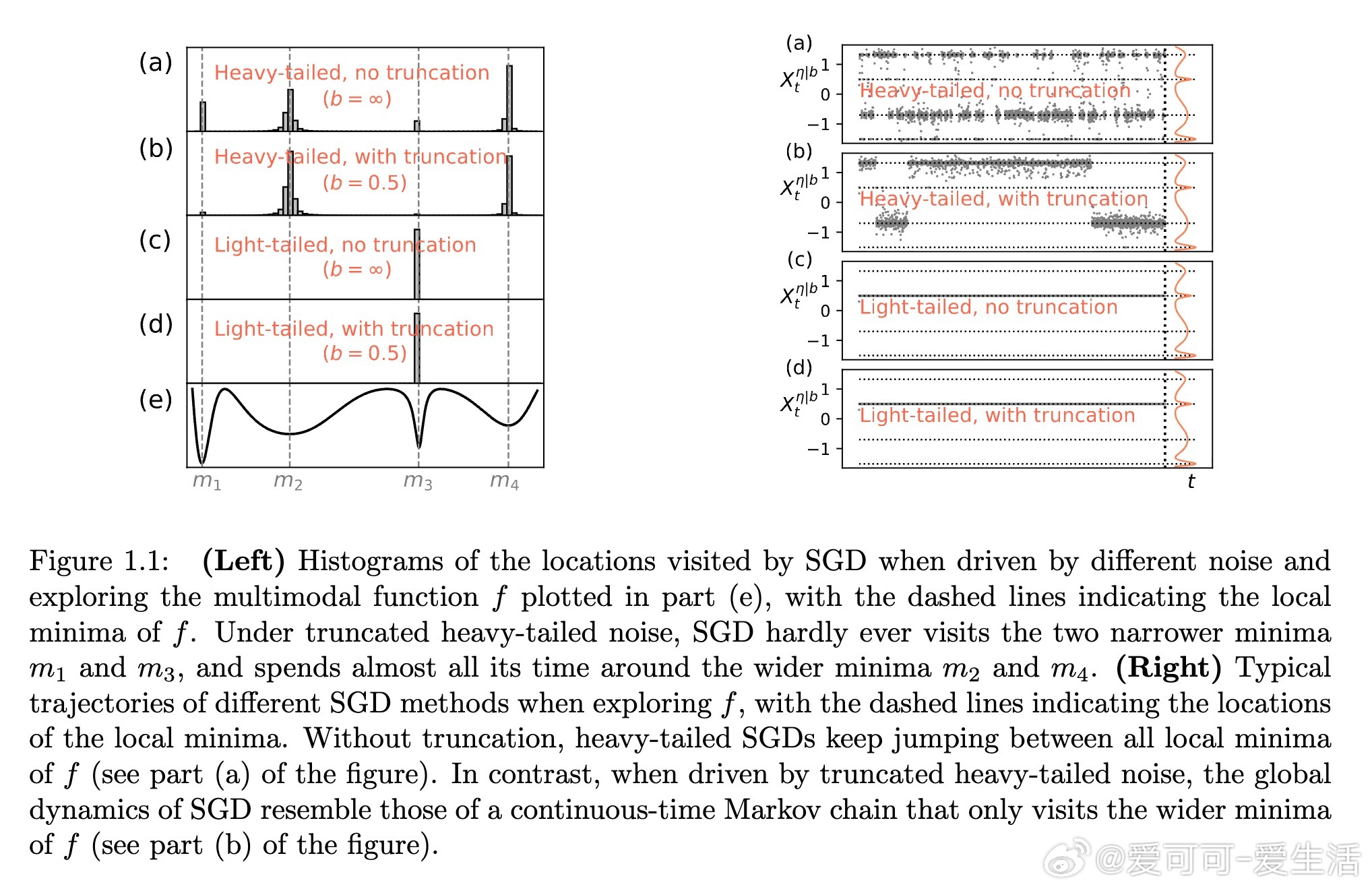
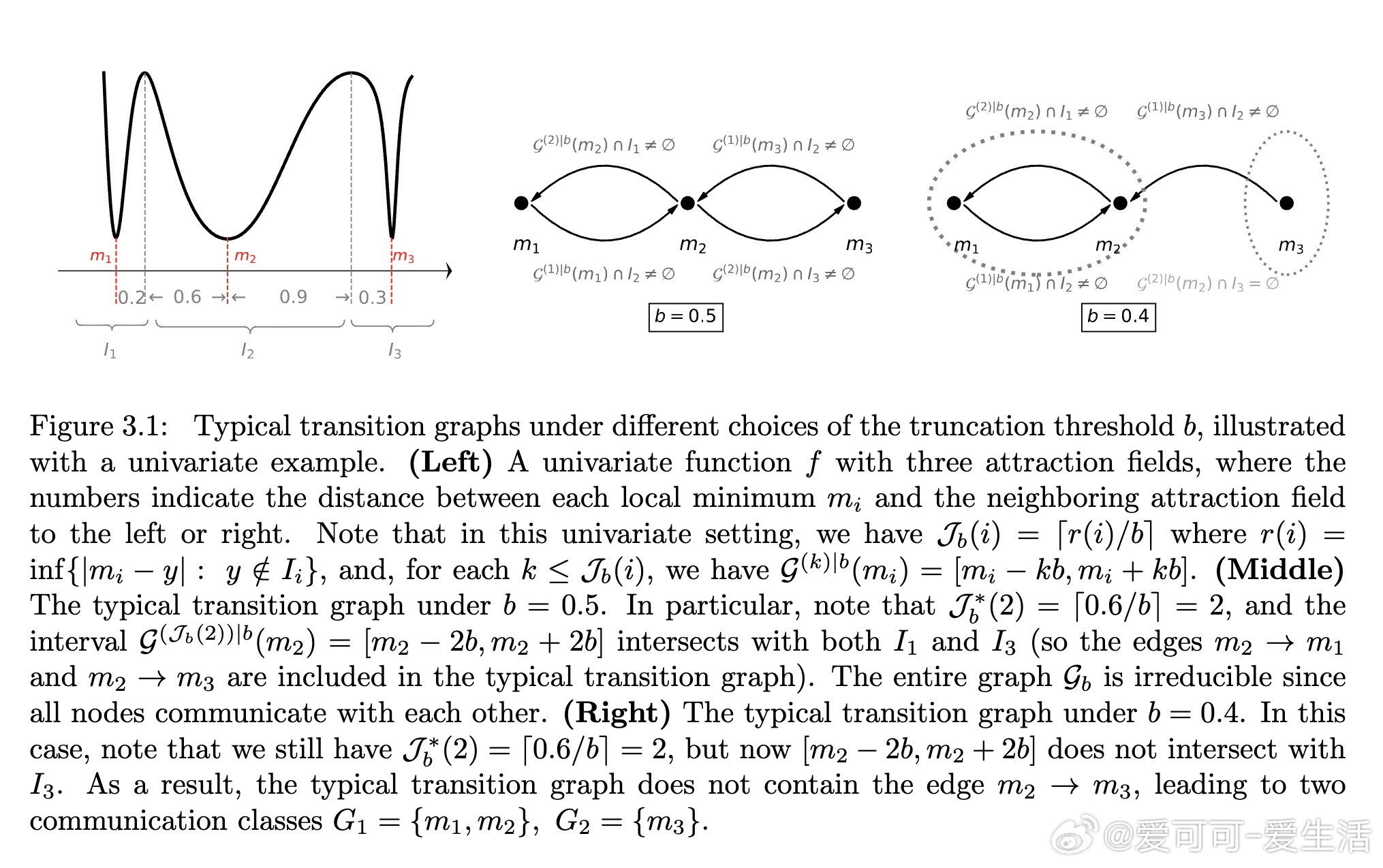
1. 理论刻画: 通过大偏差和亚稳态分析,证明截断重尾噪声驱动的SGD在适当时间尺度下的轨迹收敛到只访问最宽吸引域(即平坦极小点)的马尔可夫跳过程。相比传统轻尾噪声下指数级逃逸时间,重尾噪声下跳跃次数决定逃逸时间的多项式量级,且梯度截断强化了这一效应,几乎完全避免陷入狭窄极小点。
2. 算法设计: 基于理论发现,提出在训练阶段注入并截断重尾噪声的策略,通过调整梯度噪声的尾部分布(采用Pareto分布放大尾部),结合梯度裁剪,显著导向平坦极小点,从而提升测试集表现。实验涵盖了从基础模拟到复杂深度网络(如Wide Residual Networks)和优化器(Adam),均验证了该方法的有效性。
3. 实验验证: 在多个视觉数据集和模型架构上的对比实验显示:重尾噪声注入加梯度裁剪的SGD找到的解具有更平坦的损失几何,测试准确率和稳定性明显优于传统SGD及仅裁剪或仅注入噪声的变体。
该工作突破传统局部收敛分析,全面揭示了重尾噪声与梯度截断如何协同调控SGD的全局训练轨迹,为设计更优泛化性能的训练算法提供了坚实的理论与实践基础。
论文链接:arxiv.org/abs/2510.20905
机器学习 深度学习 优化算法 随机梯度下降 重尾噪声 泛化能力