机器之心编译

这是一次数学理论与计算机算力结合的胜利。

设想一下，如果我们的天空总是被一层厚厚的不透明云层所遮蔽，既看不见星星，也无法从上方俯瞰我们的星球，我们还能发现地球是圆的吗？

答案是肯定的。通过测量地面上特定的距离和角度，我们就能确定地球是一个球体，而不是平面或者甜甜圈状。即使没有卫星照片也能做到。

数学家们发现，这种情况在更普遍的二维曲面中也经常成立：只需要曲面上相对少量的局部信息，就足以推断出其整体形态，也就是由局部唯一确定整体。

然而在某些例外情况下，这些有限的局部信息可能对应着不止一种曲面。在过去的 150 年里，数学家们一直在致力于整理这些特例：即那些通常只能定义一种曲面，实际上却描述了多种曲面的局部测量数据。但他们能找到的唯一例外并不是像球体或甜甜圈那样规整、封闭的曲面。相反，这些曲面要么向某个方向无限延伸，要么拥有某种「边缘」。

没有人能找到一个打破这一规律的封闭曲面，似乎根本就不存在这样的特例。也许，这类曲面总是可以通过常规的局部信息被唯一确定。

如今，数学家们终于发现了一个寻觅已久的特例。在去年 10 月发表的一篇论文中，三位研究人员，包括柏林工业大学的 Alexander Bobenko、慕尼黑工业大学的 Tim Hoffmann 以及北卡罗来纳州立大学的 Andrew Sageman-Furnas，描述了一对非常扭曲的封闭曲面，它们虽然拥有相同的局部信息，却具有完全不同的全局结构。

这一发现耗费了该团队数年的辛劳、几台因运算过热的笔记本电脑，以及一个来自几何学看似无关领域的意外线索。

几何学中的异类

数学家们有各种各样的方法来局部地描述一个曲面，但其中两种尤为有用。

其中一种方法捕捉的是关于曲面「外在」曲率的信息，即在曲面上任选一点，你可以沿着无限多的方向计算曲面在空间中的弯曲程度，也就是所谓的曲率。只关注那些能得到最大和最小曲率值的方向，然后取这两个值的平均数，得到的数值被称为「平均曲率」。你可以计算曲面上任意给定点的平均曲率，从而更好地理解它是如何置于周围空间之中的。

另一种测量方法捕捉的是关于曲面「内蕴」曲率的信息，这是一种不依赖于曲面所在外部空间的几何属性。试想一张平整的纸，你可以把它卷成圆柱管而不必拉伸或撕裂它。如果纸上两点之间由一条曲线连接，那么这条曲线在圆柱上的长度将保持不变。这意味着这张纸和圆柱体拥有相同的「度量」，即距离的概念。

但如果你试着把这张纸包在球体上，情况就不再是这样了。你不得不拉伸、剪开或弄皱这张纸，点与点之间的曲线长度也会随之改变。因此，这两个曲面拥有不同的度量。

1867 年，法国数学家 Pierre Ossian Bonnet 证明，如果你知道一个曲面上每一点的度量和平均曲率，通常就足以确定该曲面的形态。当然，只是「通常」。但「通常」并不代表「总是」，正是这种不确定性让数学家们心痒难耐。

Pierre Ossian Bonnet

在 Bonnet 提出证明后的 150 年间，数学家们发现了各种违背这一规律的曲面。这些曲面拥有相同的度量和平均曲率，却不具备相同的全局结构。

但所有这些曲面都属于数学家口中的「非紧致」曲面。它们不像球体、甜甜圈以及其他「紧致」曲面那样能够完美地闭合。相反，非紧致曲面可能向某个方向无限延伸（如平面或圆柱面），或者拥有突然中断的边缘（如同从一个更大的形状上裁下来的一块）。

紧致曲面受到的限制则更多，它们必须满足各种约束条件，才能自身回转并完美闭合。因此，认为它们或许能被其度量和平均曲率唯一确定，似乎是合乎情理的推测。

1981 年，数学家 Blaine Lawson 和 Renato de Azevedo Tribuzy 证明，对于球体及任何与其拓扑等价的曲面，即任何没有孔洞的紧致曲面。这一推测确实成立。

而当涉及到带有一个孔洞的紧致曲面（即拓扑学上的「环面」，类似于甜甜圈）时，情况多了一点回旋余地。数学家们证明，给定的度量和平均曲率最多只能对应两个不同的环面。

然而，从来没有人找到过这种「紧致 Bonnet 对」的实例。因此在几十年间，学界普遍认为环面与球体一样，给定的度量和平均曲率只能定义唯一的环面。

「很长一段时间里人们都对此深信不疑，」杜克大学的 Robert Bryant 说道，「因为他们造不出任何反例。」

但是，他们错了。

像素化的世界

过去 20 年里，Alexander Bobenko 一直在啃那些「数学甜甜圈」。21 世纪初，他曾试图证明紧致 Bonnet 对确实存在。但当他意识到这个问题绝非几个月就能解决时，便将其暂时搁置，转而专注于他认为能更快取得进展的问题。

他转向了一个看似与 Bonnet 问题毫不相干的数学领域，但这恰恰成了最终解开谜题的关键。

Bobenko 开始思考「离散」曲面，这有点像是光滑曲面经过像素化处理后的低分辨率版本。数学家之所以研究离散曲面，是因为它们不仅本身具有重要的几何性质，而且在计算机科学、物理学、工程学等领域也有着广泛的实际应用。

要构建一个离散曲面，需要选取有限数量的点，并用线段将它们连接起来，形成一个由平面构成的形状。通过选择不同的点，可以用不同的方式来表示同一个光滑曲面。例如，下面就是几种表示球体的方式：

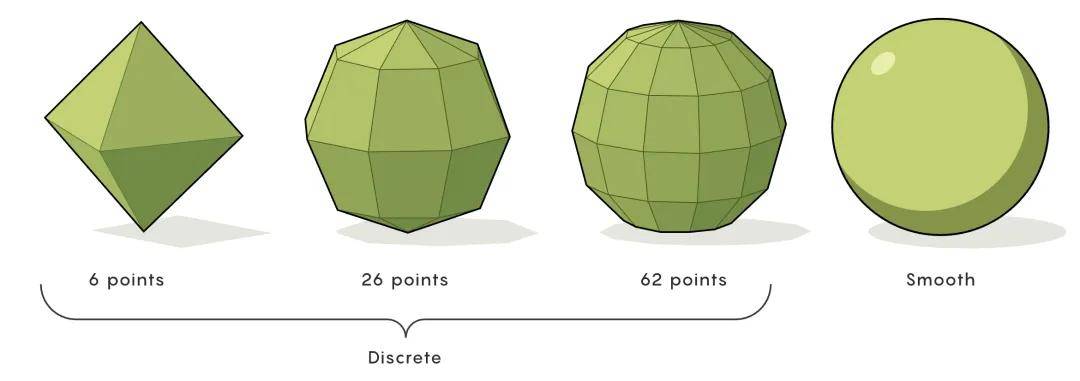
有些离散曲面能比其他的更好地进行表征。近二十年来，Bobenko 和他的长期合作伙伴 Tim Hoffmann 一直致力于建立一套理论，旨在利用离散曲面尽可能保留光滑曲面最显著的几何特征。

2010 年代，当时还是哥廷根大学博士生的 Andrew Sageman-Furnas 加入了这项工作，并将 Bonnet 问题重新带回了讨论之中。

Sageman-Furnas 对渔网等编织材料的力学机制很感兴趣，这些材料本质上就是离散曲面，这也吸引他进入了离散数学领域。在此过程中，他提出了 Bonnet 问题的一个离散版本：局部信息在什么情况下能唯一确定一个离散曲面，又在什么情况下不能？

通过调整一种已知的生成 Bonnet 定理反例的方法，Sageman-Furnas 与他的导师 Max Wardetzky 以及 Hoffmann 一起，找到了一套在离散情形下构造反例的「配方」。

与光滑情形一样，这些反例也总是非紧致的。但由于离散曲面并不包含无限多个点，因此利用计算机对其进行研究是可行的。Sageman-Furnas 不禁设想，是否可能利用计算机的「暴力求解」法，在离散几何的世界里找到一对紧致 Bonnet 对？如果确实如此，那么离散情形或许也能为解决光滑情形下的问题指明方向。

于是，他作为 Bobenko 研究组的博士后研究员来到柏林，加入了 Bobenko 和 Hoffmann 的行列，并着手开展工作。

曲面探寻之旅

2018 年春，Sageman-Furnas 开始通过计算机搜寻一种特殊的曲面，这种曲面可以被转化为一个 Bonnet 对，就像是用「老面」作为基底能烘焙出各种不同的面包一样。这个作为「引子」的曲面，类似于他读研期间用来构建离散 Bonnet 对的那些曲面。但这一次，他要求它必须是一个环面。也就是说，它必须是紧致的，且带有一个或多个孔洞。

Hoffmann 回忆称，Sageman-Furnas 消失了数周，甚至可能数月。当这位年轻的数学家终于再次现身时，他找到了他一直在寻觅的东西：一个长满尖刺的形状，与其说像环面，倒不如说更像是一只折纸犀牛。

「犀牛」。

但它确实是一个环面。根据 Sageman-Furnas 的计算机程序，它具备生成 Bonnet 对所需的所有其他属性。更重要的是，当 Sageman-Furnas 在计算机上生成这些 Bonnet 对时，它们也都是环面。从犀牛形状到 Bonnet 对的变换似乎并没有将犀牛形状扭曲成非紧致曲面。这些曲面始终保持紧致。

「当你开始进行计算探索和设计时，」Sageman-Furnas 说道，「你可以得到一些远超出你想象的新例子。」

但这会不会好得令人难以置信？计算机程序会产生舍入误差：Sageman-Furnas 的犀牛形状可能看起来符合所需的标准，它生成的 Bonnet 对也可能看起来是环面，但这都可能只是假象，是微小计算误差造成的假象。如果没有严格的证明，数学家们无法确定。

「他来了，给我们展示了一些看起来很奇怪的几何物体，看起来很像是数值计算产生的垃圾，」Bonnet 说。「开玩笑地说，我对整个项目最宝贵的贡献可能就是当时我说了一句：『我见过更糟糕的。』」

Andrew Sageman-Furnas（左）、Tim Hoffmann（中）和 Alexander Bobenko（右）构建了一对新的形状，从而解决了一个长期存在的猜想。

虽然花了一些时间，但 Hoffmann 和 Sageman-Furnas 最终确信这个「犀牛」形状值得认真研究。如果能够找到这样一个离散的 Bonnet 对的例子，那么光滑曲面的情况或许也并非毫无希望。Hoffmann 和 Sageman-Furnas 在那个夏天里仔细研究这个犀牛形状，寻找线索，有时一次视频通话就长达八到十二个小时，寻找可能有助于他们缩小光滑 Bonnet 环面搜索范围的特殊性质和几何约束。

到了九月，他们终于找到了一个非常有希望的新线索，这让 Bobenko 重新投入到他几十年前放弃的这个问题中。

闭合环路

线索与沿着犀牛边缘环绕的特定线条有关。

这些线条已知可以提供关于犀牛曲率的重要信息 —— 描绘出它弯曲和折叠程度最大和最小的方向。由于犀牛是一个存在于三维空间中的二维表面，数学家们原本预计这些线条也会在三维空间中勾勒出路径。但实际上，它们总是位于平面或球面上。这些排列如此巧合的可能性微乎其微。

「这让我们觉得一定有什么特别的事情正在发生，」Sageman-Furnas 说道。这太不可思议了。

与离散表面不同，光滑表面没有边缘。但你仍然可以绘制「曲率线」，描绘出最大和最小弯曲的路径。Sageman-Furnas、Bobenko 和 Hoffmann 决定寻找一个光滑的犀牛类比物，其曲率线同样被限制在平面或球面上。也许一个具有这些特性的初始表面可以产生光滑的 Bonnet 环面。

但这样的表面是否存在尚不清楚。

然后博本科意识到，一个多世纪前，法国数学家让・加斯顿・达布就几乎已经提出了数学家们现在需要的东西。

达布提出了生成具有正确曲率线的表面的公式。问题是，他的公式无法生成闭合的曲率线。相反，它们「看起来像螺旋线，并延伸到无穷远，」Bobenko 说。「不可能让它们闭合。」这意味着虽然曲率线可能位于平面和球面上，但整个表面不会是环面。

经过多年的努力，数学家们 —— 结合使用纸笔和计算实验 —— 终于找到了如何调整达布的公式，使曲率线闭合。他们终于找到了光滑的犀牛类比物，尽管两者看起来并不太相似。

此外，正如他们所希望的那样，这个光滑的犀牛可以生成一对新的环面，它们具有相同的平均曲率和度量数据，但整体结构不同。该团队最终找到了 Bonnet 问题的答案：某些环面最终无法通过其局部特征唯一确定。但是，当他们弄清楚这对 Bonnet 曲面究竟长什么样时，他们发现这两个环面互为镜像。「从技术上讲，这不成问题，」Sageman-Furnas 说道。「从形式上讲，它解决了问题。」但他补充说，这仍然令人不满意。

因此，在接下来的一年里，他们尝试以各种方式调整他们的光滑犀牛曲面。最终，他们意识到，如果放弃其中一组曲率线必须位于球面上的要求，他们就可以构建一个新的光滑犀牛曲面，从而达到他们的目的。然后，他们利用这个曲面生成了一对新的 Bonnet 曲面 —— 这一次，是两个非常扭曲的环面，它们显然是不同的曲面，但仍然具有相同的度量和平均曲率。

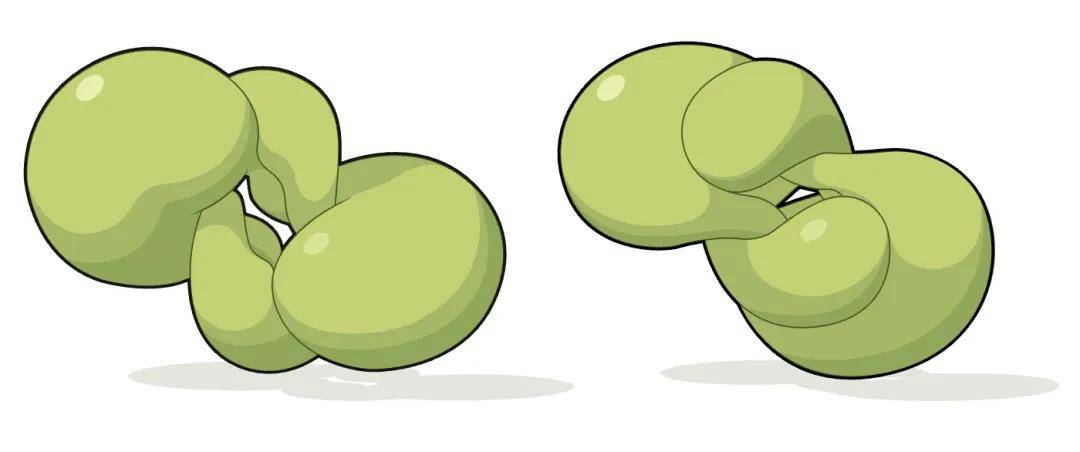
该团队最终找到了紧凑型 Bonnet 曲面的一对实例。

这一结果令 UMass Amherst（马萨诸塞大学阿默斯特分校）的数学家 Rob Kusner 感到惊讶。他表示，这表明即使是环面 —— 一些最美观、研究最透彻的曲面 —— 也并非总能用其局部特征完美描述。

「这是一个我们的直觉不够用的例子，」杜克大学的数学家 Bryant 说道。

不过，数学家们发现的这两个环面有点奇怪：它们像数字「8」一样自身相交。Bobenko 现在希望证明存在不与自身相交的 Bonnet 环面。

Bonnet 环面的发现是对 Bobenko 和 Hoffmann 数十年来在离散曲面研究方面工作的有力验证。传统上，光滑形状的几何学发展速度更快，而离散几何学的理论发展相对滞后。但在这项工作中，离散理论取得了突破性进展，并最终促成了光滑曲面方面的进展。

Hoffmann 认为，这突出表明：虽然离散曲面看起来像是其光滑对应物的简化模型，但它们拥有自身的数学生命。离散世界可以像光滑世界一样丰富，甚至更加丰富，揭示出一些可能被忽略的额外对称性和联系。

「人们似乎忘记了离散方面的研究，」Hoffmann 说道。「但我们仍然可以从中有所收获。」

原文链接：https://www.quantamagazine.org/two-twisty-shapes-resolve-a-centuries-old-topology-puzzle-20260120/